Vi forsøger såvidt muligt at motivere læringen vha. virkelighedsnære problemstillinger.
Indenfor det matematiske fagområde har det ført til en række øvelser, som både børnehavebørnene, børnehaveklassen og første klasse har kunnet deltage i.
Funktionsleg
Funktionsleg er en tegn-og-gæt leg, hvor der tegnes og gættes 3 “ting”. Den første ting er starttingen (eller input), det kan f.eks. være et brød. Den sidste ting er resultatet (eller output), det kan f.eks. være brødskiver. Imellem input og output tegnes funktionen, det ville i dette eksempel være en kniv. På denne måde introduceres funktionsbegrebet naturligt og trygt, og øvelsen kan køres forholdsvis selvstændigt af børnegruppen. Legen er ganske underholdende i sig selv, men kan derudover motiveres ved at forklare, at på de voksnes arbejdspladser bruges funktioner i vid udstrækning – her kalder man dem for processer.
Hvem sagde, børn ikke kunne tænke abstrakt?
Energibegrebet og matematisk modellering
“Wauw en fin kuglebane I har konstrueret!”. De 8-10-årige havde bygget en kuglebane, og det gav anledning til at fortælle lidt om energi.
“Hvis man nu skulle bygge en elevator til den, hvordan kunne den så se ud?”, spurgte jeg Børnene tegnede nogle skitser over, hvordan man kunne bygge en sådan.
“Hvor meget energi ville der skulle til for at løfte kuglen? Hvad ville det afhænge af?
— Kuglens vægt, svarede en af de store.
— Ja.
–Kuglebanens højde.
— Jep. Hvad med kuglens farve?
— Nej da.
— Eller kuglens temperatur?
— Nej, heller ikke.
— Ville det gøre en forskel om kuglebanen stod på Månen eller på Jorden?
— Ah! tyngdekraften!, udbrød den lille. Den er jo 6 gange svagere på Månen.
— Det kunne vi jo nok skrive op som E = mgh. […]”, konkluderede vi.
Derefter fulgte en del hovedregning (efter at vi på tallinjen havde indset, at 9.81 næsten er lig 10).
Senere faldt snakken bl.a. på atom-energi, om at lave masse om til energi og vi fik regnet på lyshastigheder.
Udfaldsrum
Et meget nyttigt begreb at have til rådighed når man leger med kort eller terninger er udfaldsrummet. Hvis jeg i Casino Pirate (en forenklet form for Black Jack) trækker en 6’er, hvad er så sandsynligheden for, at jeg overskrider grænsen på 7.5, hvis jeg trækker et kort til? Kan det bedst betale sig at angribe i Risk eller bør man forsvare? Hvilket våben skal jeg angribe med i Battle for Wesnoth?

Og børnene finder sågar nogle gange på at lave deres egne spil.
Hvordan kan den flyve?
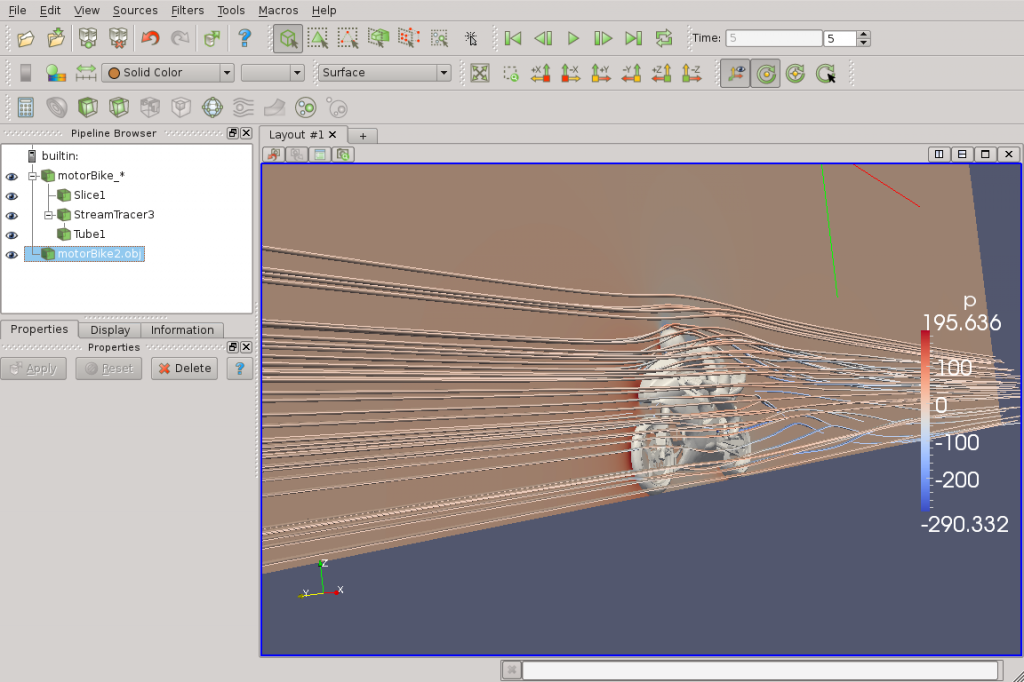
De fleste børn undrer sig på et eller andet tidspunkt over, hvordan man kan få ting til at flyve gennem luften. En god forklaring er at finde på NASAs hjemmeside, men den kræver en indsats at formidle til børn. Heldigvis får man meget foræret ved at bruge frit tilgængelige værktøjer såsom OpenFoam og Paraview, og så er der ellers åbnet op for introducere energibegrebet (igen), bevarelsesligninger (energi og moment) og endda finite element metoden.
Magiske farvelægninger
eller coloriages magiques som de hedder på fransk (praktisk søgeudtryk ifm. søgnigner på nettet) er tegninger, der farvelægges ifølge en foreskrevet kode. Denne kode kan f.eks. være i form af regnestykker, hvor f.eks. alle de stykker der giver 5 males blå, de stykker der giver 8 males røde osv.
Modellering og Programmering
Det seneste skud på stammen i matematikundervisningen er udsprunget af børnenes interesse for at lave computerprogrammer. Dels har vi leget en del med Scratch, og er derudover begyndt at løse opgaver fra en af vores matematikbøger vha. modelleringsprogrammet Octave.
Næste skridt
Fremover er der utrolig mange spor at afsøge. Bl.a. ville en generel opkvalificering af matematikkompetencerne i gruppen være til gavn. Derudover ville et større fokus på selve modeleringsaspektet af matematikken og dermed en mere anvendelsesmotiveret tilgang på sigt både sikre fagets relevans og gøre det mere tilgængeligt for alle.
I den sammenhæng er det værd at prøve, om ikke kurser såsom Model Thinking kunne bruges.
