Det er ikke altid helt let at introducere matematiske begreber naturligt i undervisningen, og måske i særlig grad, når man som på Den dansk-franske Skole tager udgangspunkt i børnenes motivation og egne interesser.
Med spillet Battle for Wesnoth har vi dog fundet en lille guldgrube af relevante og motiverende problemstillinger. Spillet er et turbaseret strategispil, der kan spilles i single eller multiplayer mode. De fleste scenarier gælder om at slå modstanderens enheder. Dette gøres ved at man selv rekrutterer egne enheder, finanseret af de landsbyer man ejer, og derefter sender dem i kamp.
Med lidt hjælp i starten (f.eks. fra de større børn) kan spillet spilles fra barnet er ca. 4.
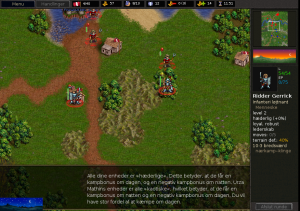
Her følger en række eksempler
En vigtig faktor i spillet er ens beholdning af guldmønter. Har man guld kan man rekruttere, har man ikke, må man håbe på at man kan klare sig med de enheder man har. Børnene får meget hurtigt en fornemmelse for tallet, som oftest ligger et sted mellem minus 10 og +100, men som iblandt når op på flere tusinde.
Det er alletiders lejlighed til at lære dem tallene fra 0 til 100, 1000 eller derover.
Det er også en oplagt lejlighed til at introducere addition, substraktion og multiplikation. Hvis jeg har 25 guldmønter og tjener 12 i denne runde, hvor mange har jeg så i næste? Og hvis jeg har 25 guldmønter og køber en bueskytte, der koster 14, hvor mange har jeg så tilbage?
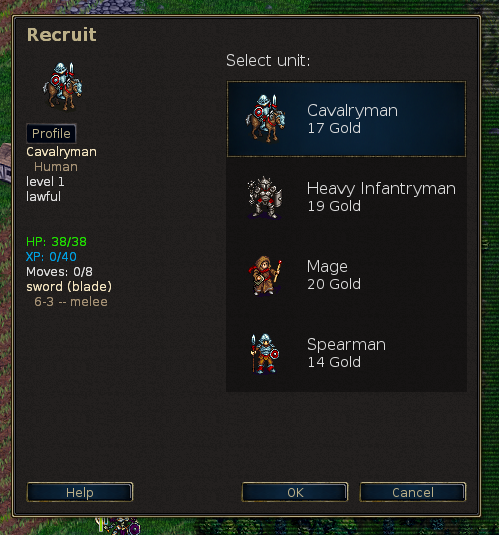 Hvis jeg har 8 landsbyer og tjener 2 guldmønter per stk, hvor mange guldmønter tjener jeg så?
Hvis jeg har 8 landsbyer og tjener 2 guldmønter per stk, hvor mange guldmønter tjener jeg så?
Et andet særligt fængende element i spillet er, at enhederne vinder erfaring når de kæmper, og når de har erfaring nok stiger de i niveau (de “bliver seje”). Relevante spørgsmål her er: hvis min enhed bliver sej ved 75 EP og jeg lige nu har 64, hvor mange EP mangler jeg så?
Eller: fjendtlige enheder giver mig 8 EP per niveau hvis jeg kan slå dem. Hvor mange EP giver en fjendtlig level 3 enhed så? Man får hurtigt brug for sine multiplikationstabeller.
Og hvad med denne: orkarmbrøstskytter (stav lige til den .) har 3 skud der hver gør 8 i skade. Hvor meget skade kan de så maksimalt gøre? Hvad er sandsynligheden for, at det sker, hvis hvert skud har 60% sandsynlighed for at ramme?
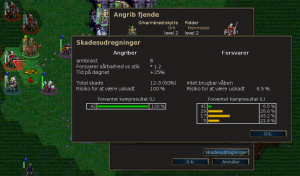
Således kan man for de lidt større på denne måde introducere procenter og sandsynlighedsfordelinger, alt sammen meget konkret og håndgribeligt.
