It was back towards the end of last century, and most of us didn’t really grasp what we were supposed to make of it. It didn’t seem to be of any concern whether the teaching was motivating or not, nor whether the time the children invested in the learning eventually was worth it. In the math lessons we were told that…
1. the cosine is used to calculate the length of the edges in a triangle…
… which no-one really has done for ages.
What you actually do use the cosine and sine for is to describe circular movements: cos(t) and sin(t) are respectively the x and the y coordinate of a point having moved t length units along the unit circle. From a practical perspective that can be used for instance to write a program that displays a clock.
Playing around with the code in line 7 and 8 gives a good hands-on understanding of the parameters in the expression
C + A·cos(ωt + φ),
i.e. the meaning of:
- the amplitude A: the length of the hands of the watch
- the frequency ω: the speed at which they rotate (one of them is 12 times faster than the other) ¹
- the phase φ: at what time they start (in this case 12 o’clock, at -90°)
- the offset C: where the center of the clock is.
Pushing it a little further, the concept can be used to convey an understanding of signals, frequencies and spectra, be it sound signals, light waves, simple alternating currents, rotating wheels and much more.
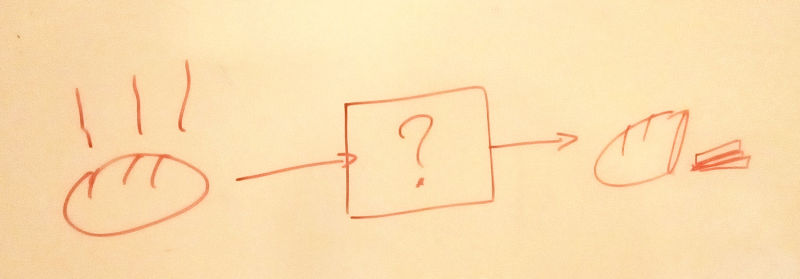
Interestingly, the kids are quite receptive to the notion of a (Fourier) spectrum. For instance, the spectrum of an F major chord on our piano looks like this:
You can also explain the children what a low-pass filter is by playing a high-pitched tone (~13kHz) on a computer: the kids will hold their ears in pain while most adults won’t be able to hear it at all. Very funny!
2. a function is something involving a graph…
…something with “ax+b”, which is not completely wrong per se, but nonetheless a serious under-statement of the importance of the concept of a function.
Indeed, considering functions as the fundamental building blocks of modeling – the Swiss army knife of abstract thinking so to speak – completely changes the perspective. A function associates an output with an input, no more, no less. When you have formulated your function – your model – you have identified what is relevant, and discarded what was irrelevant. That can be unfathomably important:
From then on you will begin to see relations of causality, predict events and progress, compare the predicted with the observed, chain functions together, understand what is happening, act intelligently, adapt and improve, share your understanding with others.
Within the natural sciences the concept is omnipresent. Physicist tend to refer to it as operators.
Large organizations are barely manageable without it nowadays. In business language functions are often referred to as processes.
A great tool for introducing the concept of a function to children (4+) is the function builder, a tool allowing to visually build and play with functions that transforms an input (on the left) to an output (on the right):
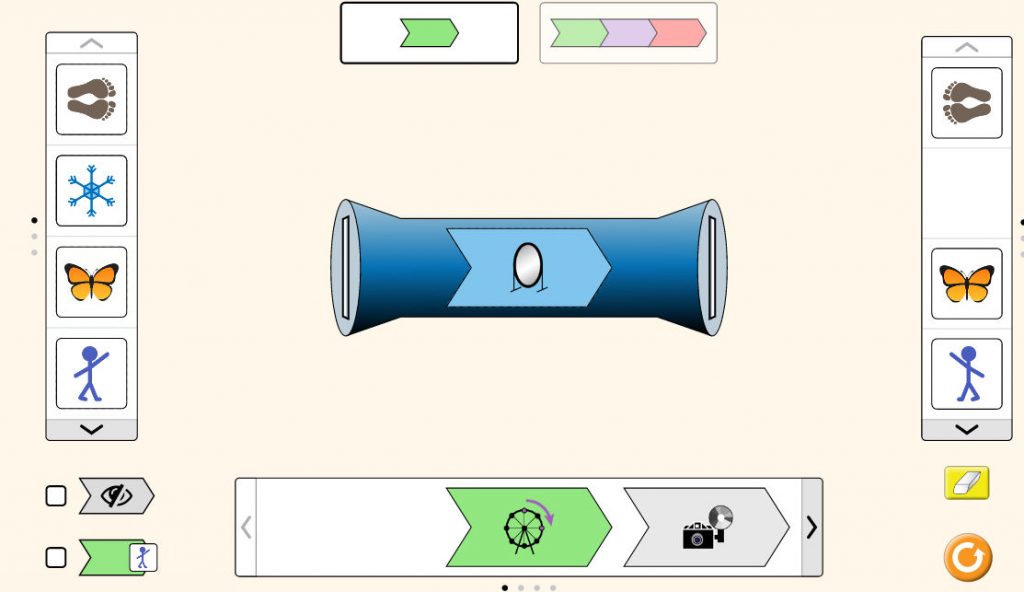
At the school we sometimes organize a function-Pictionary:
“If the input is… [drawing] a bread, and the output is… [drawing] slices, then the function is probably… a knife!”
3. differential equations are solved using obscure rules learned by heart…
… and aren’t of much use after all, as most people who learned about them in high-school will recall (hint: “coefficients in a complex-valued function”). What should have been the great epiphany concluding 13 painful years on the school bench ended up as a complete anti-climax for the vast majority.
But in reality it’s quite simple: once you have formulated your model using functions, you generally want to know how it behaves under different circumstances (inputs). The interesting models are often so complex that simply entering the input into a formula won’t work – one has to work out the final result in small pieces at the time. These small different pieces (differences) are added up (integrated) into a solution, nowadays in practice always using a computer.
From a pedagogical perspective the classical Euler method is quite suitable and can be used from age ~6 and up, see the first order example (x’ = ±1) below²:
In the example, the velocity v=1 of the cloud is constant until the cloud reaches sufficiently far out on the right (x>250), after which the velocity changes sign until it reaches sufficiently far left (x<150), after which it changes sign and so forth. In each iteration of the draw loop, v is added to the position x, giving the new position ³.
The slightly older children can use differential equations to answer truly relevant questions, such as calculating the time it takes a space ship to travel to Mars:
In most of the examples above, one skill has turned out to significantly leverage the fun and relevance of math: programming. And so it turns out that math can be easy after all!
So stop whining.
Footnotes:
¹ Strictly speaking, ω is the angular frequency, i.e. ω=2πf where f is the frequency expressed in Hz.
² The example isn’t actually a true first order differential equation (DE), since there doesn’t exist a function f such that x’=f(x), since for a given value of x ∈ [150, 250], x’ can take on two values, 1 and -1. As it would often be the case when solving actual real-world problems, we are cheating a little: here we are using an extra variable (v) to store more information than what a first order system can hold. In order to solve the problem within a strict DE framework, one would need a second order equation involving Dirac delta functions, as in the flying pig example (code here).
³ Formally, rather than adding v we would need to add Δx, the distance traveled during a short time Δt, i.e. Δx=v·Δt. Here it works because we assume Δt=1.